
In this modern age and digital economy, cryptography is the foundation of any secure message exchange. However, the issues relating to quantum computing present strong challenges to the conventional method of cryptography. Post Quantum Cryptography or PQC is a new and developing branch of cryptography that is focused on making new cryptographic algorithms that will be resistant to quantum age.
Why is Post-Quantum Cryptography Important?
Current cryptographic standards mainly include RSA, ECC (Elliptic Curve Cryptography) and DSA. Their security is based on mathematical problems like integer factorization and discrete logarithms. In the case of classical computers, they are infeasible computationally, but for quantum computers which can perform exponential computations parallelly, breaking the systems would be easy with algorithms such as Shor’s algorithm.
It makes critical data, such as financial transactions, medical records and classified information susceptible to attack. Post Quantum Cryptography is aimed at finding ways of creating encryption methods that prove secure against quantum computers, thus having future-proof security in sensitive information.
Core Categories of PQC Algorithms
PQC-based algorithms can broadly be categorized into several main categories based on the basic mathematical principles they rely on:
1. Lattice-Based Cryptography
Relies on issues like the shortest vector problems such as the SVP and learning with errors such as LWE that even quantum computers cannot solve.
➢ Advantages:
High efficiency and scalability are among the benefits of using the existing solutions, found to erect a sustainable organizational support structure for effectively executing the change management process. Kyber for encryption and Dilithium for digital signatures are the leading contenders.
➢ Applications:
Encrypted communications, code validation and data encryption.
2. Code-Based Cryptography

This approach involves the usage of error correcting codes which form part of the cryptographic primitives. Extends the hardness of decoding random linear codes.
➢ Advantages:
Security is backed up by extensive research of more than 30 years. One of the examples of the HDPCs is a Classic McEliece.
➢ Applications:
Mainly encryption but can also employ signatures which are in the digital world.
3. Hash-Based Cryptography
These algorithms are quantum-safe cryptographic methods based on the hardness of inverting cryptographic hash functions. Creates signatures with the help of hash functions.
➢ Advantages:
Easy to understand, supported by research and very safe. That is why we have examples of such an approach, for instance, SPHINCS+.
➢ Applications:
Digital signatures for systems that are secure over time.
4. Multivariate Quadratic Equations
Multivariate Quadratic Equations (MQ) are a kind of mathematical problem that serves as the foundation for solving Multivariate Quadratic Cryptography which is among the categories of Post-Quantum Cryptography (PQC). These equations include polynomials with variable terms, the degree of which is two, multiple-variable and are notorious for their computation intensity thus, ideal for cryptography in a post-quantum world.
➢ Advantages:
The high efficiency of the signatures schemes. It is significant to note that Rainbow is an algorithm in this field.
➢ Applications:
Digital signatures.
5. Isogeny-Based Cryptography
Isogeny-based cryptography is an exciting area in post-quantum cryptography that relies on the mathematical structure of isogenies of elliptic curves. It provides compact key sizes and is best for secure communications with restricted bandwidth.
➢ Advantages:
Compact key sizes, which are useful in constrained environments. Examples include SIKE (Supersingular Isogeny Key Encapsulation).
➢ Applications:
Secure key exchange.
6. Symmetric-Key Quantum Resistance
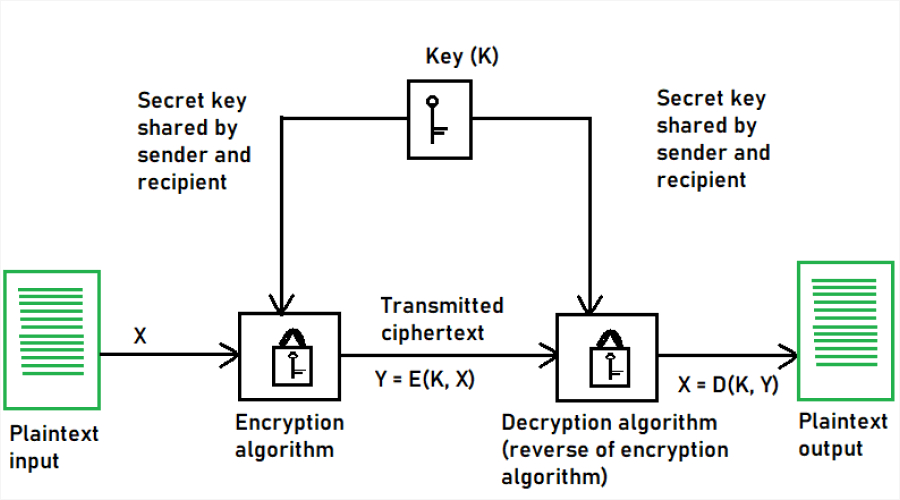
Symmetric-key quantum Resistance refers to the resistance of symmetric-key cryptographic algorithms against attacks by a quantum computer. In contrast to public key cryptography, symmetric systems are less prone to the exponential speedup provided for certain mathematical problems by quantum computers.
➢ Advantages:
Minimal changes are needed to existing systems.
➢ Applications:
General cryptographic systems.
Challenges and Considerations in Post-Quantum Cryptography (PQC) Algorithms
There are several issues and risks associated with the use and integration of Post-Quantum Cryptography (PQC) algorithms. These challenges arise due to endeavors to seek security, optimal performance and compatibility in migrating to a post-quantum cryptographic environment.
➜ Security Assumptions
The preservation of PQC algorithms is anchored on mathematical problems such as lattice problems or multivariate polynomials considered hard to solve for quantum computers. However, these assumptions are not as yet as well-tested as are the modern preserve RSA and ECC’s.
➜ Performance
Some of the common issues that arise out of PQC algorithms include the fact that the public parameters of such schemes as well as the ciphertexts are usually larger than that associated with classical schemes. For instance, post-quantum lattice-based schemes such as Kyber and Dilithium have key sizes several folds larger than mainstream RSA or ECC keys, which aggravates storage and communicational costs.
➜ Compatibility and Interoperability
The switchover to implement PQC therefore means readjusting and redesigning cryptographic systems in virtually every application, from browsers and email clients to smart homes, IoT devices and critical industrial systems. The recent PQC algorithms may be of larger key sizes or require higher computations that may not be supported by legacy systems.
➜ Hybrid Cryptography
Hybrid schemes combine classical and PQC algorithms for a smooth transition. Thus, the challenge is to design efficient hybrid protocol designs, without introducing any new vulnerabilities.
➜ Standardization and Adoption
Such efforts as the NIST PQC competition aim to identify good, practical and secure algorithms to standardize. The diversity of candidates (lattice-based, hash-based, code-based, etc.) complicates consensus on which algorithms to adopt.
Considerations for Successful PQC Adoption
To ensure the security of data and communication, organizations and governments all over the country have to start implementing PQC. Steps to take include:
- Prioritizing Use Cases: The essential step is to determine which system or data requires protection from quantum threats right now (Government, Financial, Healthcare, etc.).
- Early Testing: Carry out trials for the PQC algorithm in legacy systems that include performance, integration and security. Perform pilot studies using PQC algorithms in established structures as a way of determining the effectiveness of the algorithms.
- Education and Awareness: Broaden the understanding of quantum risks and the need for the move towards PQC. Ensure that cryptographic professionals are trained in how to put in place and sustain PQC systems.
- Post-Standardization: Other bodies including NIST develop specific standards and organizations should incorporate recommended algorithms into their operations as they eliminate the weaker ones.
- Hybrid Approaches: Employ dual protocols up the time when quantum supremacy is effectively a threat and when both the old and new encryption strategies are viable.
- Continuous Research: New research topics include analysis of new and unidentified Quantum Attacks, refining PQC algorithms and devising more efficient Cryptographic primitives.
Conclusion
In conclusion, It is of paramount importance in ensuring digital systems safety against the risks quantum computers may pose. It relies on mathematical problems resistant to attack by quantum computers and hence PQC is the means to make digitally sensitive information safe in a world dominated by quantum computing. As quantum computing is placed under development, it will be essential to transition to PQC to protect the global infrastructure. It will then make possible a resilient, secure future for digital communications and transactions.






